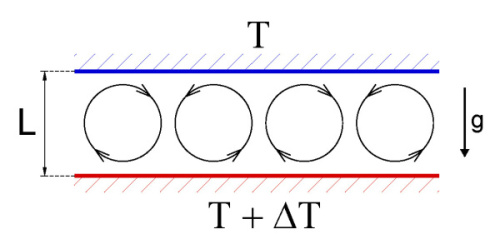
Figure 1: Schematic representation of Rayleigh-Bénard convection
Turbulent free convection plays a prominent role in the heat transport within atmospheric and oceanic circulation, geodynamics, stellar convection and industry. A model for fundamental convection studies is the Rayleigh-Bénard convection.
Rayleigh-Bénard convection is defined as a thermally driven flow in a fluid layer between two infinite rigid horizontal plates, where constant temperatures are imposed on both fluid boundaries. The bottom plate is heated and the top one is cooled. The hotter liquid at the bottom expands and produces an unstable density gradient in the fluid layer (in gravitational fields). If the density gradient is sufficiently strong, the hot fluid will rise up, onset a convective flow which results in an enhanced transport of heat between the two plates. The basic issue is to find a relation between a heat flux H and the temperature difference DT between the bottom and top plates.

Figure 1: Schematic representation of Rayleigh-Bénard convection
Control parameters of Rayleigh-Bénard convection:
|
Rayleigh number |
Ra = g aΔT L3/vk |
ratio between thermal driving forces and viscous
dissipative forces |
|
Prandtl number |
Pr = v/k |
controls relative thickness of momentum and thermal
boundary layers |
|
Nusselt number |
Nu = H/H0 |
measure of enhancement of heat transfer by
convection in comparison with the conductive transfer in still fluid |
|
|
g |
acceleration due to gravity |
|
|
a |
isobaric thermal expansion coefficient |
|
|
ΔT |
vertical
temperature difference |
|
|
L |
vertical dimension of the convecting fluid layer |
|
|
v, k, l |
kinematic viscosity, thermal diffusivity, thermal
conductivity |
|
|
H |
heat flux transferred by thermal convection |
|
|
H0 = lΔT/L |
conductive heat flux (heat flux by diffusion in a
still fluid) |
|
Boussinesq condition |
aΔT << 1 |
in experiments with gaseous fluids the condition
justifies the assumption of “incompressibility” of the fluid |
|
Scaling law |
Nu=f(Ra,Pr) |
relation between a heat flux H and the
temperature difference ΔT expressed by nondimensional numbers |
The cryostat configuration is typical for low loss NMR magnet cryostats. Liquid nitrogen (LN2) vessel (60 litres) is situated above liquid helium (LHe) vessel (28 litres) and convection cell (21 litres of cold helium gas). Convection cell is thermally connected with LHe vessel by a heat exchange chamber with an adjustable pressure filled by gaseous He. Radiation heat flux from outer wall to LN2 vessel is reduced by the thermal shield that is cooled by cold gaseous nitrogen. The convection cell is shielded by a copper shield which is cooled by liquid He. Basic evaporation rates of LN2 and LHe are 5 l/day and 1.2 l/day, respectively.
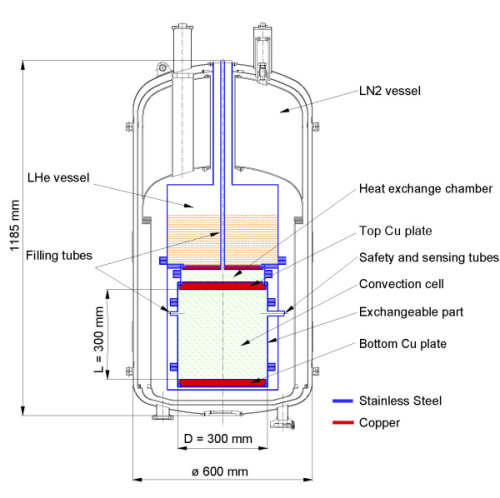
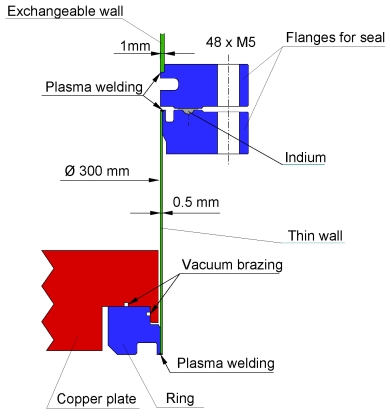
Figure 3: Cryostat and detail of bottom part of the convection cell
Parameters:
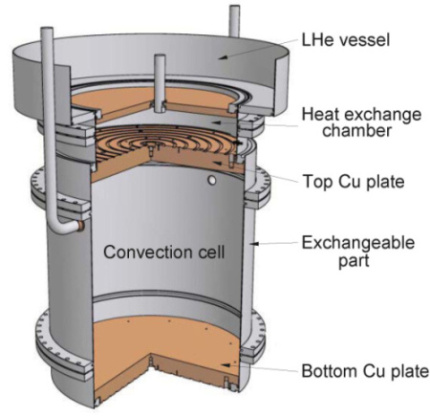

Figure 3: Convection cell
P. Urban, P. Hanzelka, V. Musilová, A. Srnka, L. Skrbek: Design and Tests of the Cryostat with an Experimental Cell for Turbulent Thermal Convection. Proceedings of the Colloquium Fluid Dynamics 2007. Praha: Institute of thermomechanics ASCR, v. v. i, 2007. S. 93-94. ISBN 978-80-87012-07-9.
A. Srnka , P. Hanzelka , V. Musilova., P. Urban, L. Skrbek: Design of a Helium Cryostat for the Study of Turbulent Thermal Convection at Cryogenic Temperatures. CryoPrague 2006 - Proceedings of the 21st International Cryogenic Engineering Conference. Praha: Icaris Ltd (2006) 661-664. ISBN 978-80-239-8883-3.
Pavel Urban, Crygenics group
Institute of Scientific Instruments ASCR, v.v.i.
Czech Republic