ON DIRECT ALGEBRAIC IDENTIFICATION OF INHOMOGENEITY FUNCTIONS IN MRS

Hana Kucharova, Ales Gottvald

Institute of Scientific Instruments, Academy of Sciences of the CR,
Kralovopolska 147, CZ-612 64 Brno, Czech Republic
E-MAIL: hanca@isibrno.cz, gott@isibrno.cz
Internet: http://www.isibrno.cz/~hanca/index.html, ../~gott/index.html

Abstract: Inhomogeneity functions w(t) and W(v) := F[w(t)] are major structures for incorporating inhomogeneity phenomena into qualitative and quantitative analysis of experimental data in MR-Spectroscopy [1 - 6]. Identification of the inhomogeneity functions is a natural generalization of conventional "shimming" or "tuning" operations well known to every MR-spectroscopist. Some non-Fourier quantification methodologies in MRS are intrinsically capable of incorporating any inhomogeneity function [3]. Hence, various inhomogeneity phenomena may be separated from the signals and the spectra. Being given a reference FID-signal z := x(t,.) and an identification FID-signal u := u(t,.), the inhomogeneity function may be identified directly from experimental data.

Direct Algebraic Identification (DAI) comprises the simplest non-parametric method of determining the cartesian components, modules and phases of inhomogeneity functions. Let z := x + i y and u := u_x + i u_y be "homogeneous" (reference) and "inhomogeneous" (identification) complex FID-signals, respectively. If the distorting functions n(t), h(t), a(t) may be omitted in a generalized FID-model (see also an accompanying paper), the relation
u(t) = w(t) z(t) provides the following two linear equations for the real and the imaginary component of w := w_x + i w_y in the time-domain:

u_x = w_x x - w_y y, u_y = w_y x + w_x y (1)

At every regular time-point where |z| := x² + y² <> 0, this system has a unique solution:

w_x = (u_x x + u_y y) / (x² + y²), w_y = (u_y x + u_x y) / (x² + y²) (2)

and the module |w| and phase q_w of the inhomogeneity function may be evaluated as:

|w| = (w_x² + w_y²)^1/2, q_w = arctg (w_y / w_x) (3)

Using real-world experimental data, we verified that DAI works properly for singlets with sufficiently low noise and phase distortions (see Fig. 1). As well known, this is a typical regime for inhomogeneity shimming in MRS. For multiplets with some stronger noise and phase distortions, DAI is prone to artifacts [6], though some useful results may be still obtained in many practical cases (Fig. 2). Elimination of these artifacts is usually straightforward using spectra segmentation, phasing and filtering. Consequently, the inhomogeneity-associated prior information may be advantageously incorporated into MR-practice (spectra deconvolutions, difference spectroscopy, some non-Fourier quantifications, etc.).

References:
[1] Malczyk R., Gottvald A.: "Modelling Inhomogeneity Phenomena in MRS". In: Proc. of the International 13th BIOSIGNAL Conference, Brno, 1996, pp. 95 - 97
[2] Kucharova H., Gottvald A.: "Identifying Inhomogeneity Functions in MRS". In: Proc. of the International 13th BIOSIGNAL Conference, Brno, 1996, pp. 92 - 94
[3] Gottvald A.: "A Survey of Inverse Problems, Meta-Evolutionary Optimization and Bayesian Statistics: Applications to In Vivo MRS". Int. J. of Appl. Electromagnetics and Mechanics, 1996/97 (accepted)
[4] Taquin J.: "Line-shape and resolution enhancement of high-resolution F.T.N.M.R. in an inhomogeneous magnetic field". Revue de Physique Apliquee 14, 1979, pp. 669 - 681.
[5] Chmurny G. N. - Hoult D.: "The Ancient and Honourable Art of Shimming". Concepts in Magnetic Resonance, 2, 1990, 131 - 149
[6] H. Barjat et al.: "Reference Deconvolution Using Multiplet Reference Signals". J. Magn. Reson. A, 116, 1995, 206 - 214

Acknowledgment: This work was supported in part by GA CR, grant # 102/95/0282.

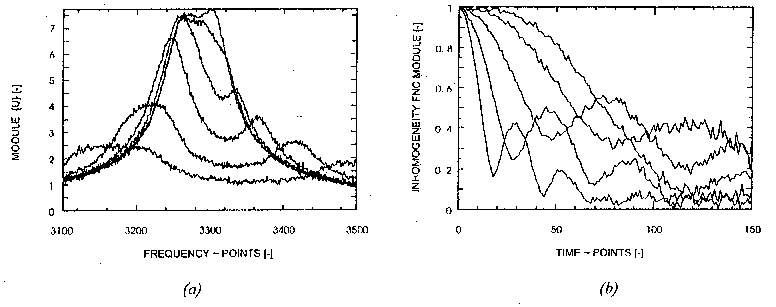
Fig. 1: Identifying inhomogeneity functions from 1-line ³¹P-spectra (H₃PO₄) using experimental data. (a) Distorted spectral lines (modules) corresponding to different magnetic field inhomogeneities. (b) Modules of the individual inhomogeneity functions, corresponding to previous spectral lines.

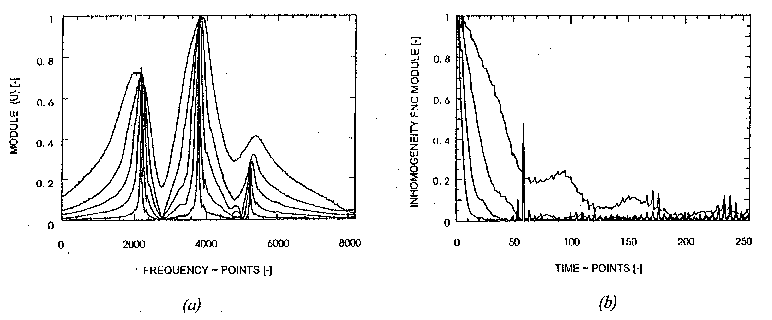
Fig. 2: Identifying inhomogeneity functions from 3-line ¹H-spectra (a mixture of acetone, H₂O and DSS) using experimental data. (a) Distorted spectral lines (modules), for different magnetic field inhomogeneities; all spectral lines are normalized to max. (b) Modules of the individual inhomogeneity functions, corresponding to previous spectral lines. As associated FID-signals are rapidly oscillating interferograms, this identification is rather demanding for the direct algebraic method. Even in this hard case, the inhomogeneity functions show only simple artifacts that are well treatable using standard operations of segmentation, phasing, smoothing or filtering.

Back to:

GIOM

Selected publications