From a mathematical point of view, we are facing to a typical inverse problem (ill-posed problems in the sense of Hadamard). Associated optimization formulation may be stated as follows:

where u* is the input data-vector (a sampled FID-signal, experimental or synthetic), x e Rn are the parameters to be determined, u(x) is a parametric model (in our case - associated with a generalized FID-signal), |.| is a norm, and a configuration manifold X is defined by a set of constraints (equations and inequalities).

Uncertainty of solutions is an inherent feature of inverse problems. For every inverse problem, there exist some natural physical limits for the accuracy of parameter estimates. These fundamental statistical limits (e.g., Cramer-Rao lower bounds) cannot be superseded in any way without using some additional prior information. Consequently, the major "secret" of solving the inverse problems consists in identifying and applying all forms of prior information - both hidden and explicit. It may be shown [6] that important prior information is associated with all structural elements in (1), including the noise-associated norm |.|, constraints defining x e Rn, etc. For strongly distorted signals, an important prior information is involved in the parametric model itself (see accompanying two abstracts). In our approach, inhomogeneity-asociated prior information is neither "guessed" nor "neglected", but identified using experimental data. This identification operation actually reduces a number of degrees of freedom to be determined via the optimization or inversion (1).

Meta-Evolutionary optimization [6] is a stochastic optimization method inspired by a biological evolution of species. In contrast to standard stochastic optimizations (Evolution Strategy, Simulated Annealing, Genetic Algorithms), this meta-method provides some additional quarantees: enforced global convergence, reduced sensitivity to initial parameter estimates, and detailed uncertainty analysis (inversion errors, total accuracy estimates, fundamental statistical limits). When being linked to a Bayesian formulation, noise features (and some probabilistic prior information) may be respected. For example, an additive Gaussian white noise in the data may be related to a Maximum Likelihood Estimation using L2-norm. A Bayesian Statistic is than generated by sampling an associated error function f(x) with the Meta-Evolutionary optimizer.

An example of the evolutionary quantification, for a 31P In Vivo MR-spectrum of a human's brain, is indicated in Fig. 1. In this case, a synthetic spectrum with strong inhomogeneity and noise artifacts has been optimally restored, in terms of the most likely estimates for 21 spectral parameters. The difference between the conventional DFT-based spectrum (Fig. 1b) and its optimally reconstructed version (Fig. 1d) is remarkable. It illustrates that even a rough specification of prior information is clearly preferable to its full negligence or an ad hoc choice (as typical for a conventional DFT-based quantification).

References:
[1] de Beer R. - van Ormondt D.: "Analysis of NMR Data Using Time Domain Fitting Procedures". NMR - Basic Concepts and Progress, Springer-Verlag, Berlin, 1992, pp. 202 - 248
[2] Haselgrove J. C. et al.: "Analysis of In Vivo NMR Spectra". Reviews of Magn. Reson. in Medicine 2, 2, 1987, pp. 167 - 222
[3] Bretthorst G. L.: "Bayesian Analysis. ...", J. Magn. Reson. 88 (1990), 533 - 551
[4] Kotyk J. J. et al.: "Comparison of Fourier and Bayesian Analysis of NMR Signals". Part I. - J. Magn. Reson. 98, 1992, pp. 483 - 500; Part II. - J. Magn Reson. A 116, 1995, pp. 1 - 9
[5] Johnson G. et al.: "Multiple-Window Spectrum Estimation Applied to in Vivo NMR Spectroscopy". J. Magn. Reson. B 110, 1996, pp. 138 - 149
[6] Gottvald A.: "A Survey of Inverse Methodologies, Meta-Evolutionary Optimization and Bayesian Statistics: Applications to In Vivo MRS". Intnl. J. of Appl. Electromagnetics and Mechanics, 1996/97 (accepted)

Acknowledgment: This work was supported in part by GA CR, grant # 102/95/0282.

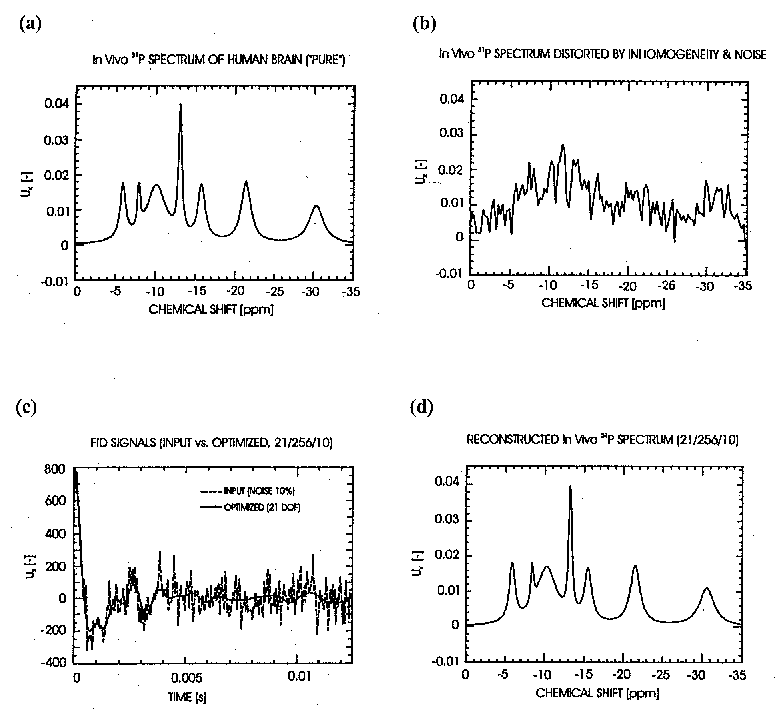
Fig. 1: The most likely reconstruction of a synthetic In Vivo 31P-spectrum (real part) with strong inhomogeneity and noise distortions. (a) An ideal "pure" spectrum. (b) Standard DFT-spectrum with inhomogeneity and noise distortions, without apodization. (c) Time-domain signals - input noisy data and reconstructed optimal signal. (d) Reconstructed spectrum - inhomogeneity and noise distortions eliminated. Conditions: 21 spectral parameters determined via Meta-Evolutionary Bayesian Statistics, imposing only insignificant soft constraints on resonant frequencies, amplitudes and phases (relaxation rates fixed). Real parts of the signal and the spectra are shown. Number of complex data-values: 256. Noise: white Gaussian, 10 % of the maximal signal amplitude. Synthetic FID-signals generated from experimental parameters given in [2], using an ad hoc inhomogeneity function. For 20 Meta-optimization loops, this inversion requires CPU-time ~ 100 seconds/1 MFLOPS.

---

Back to:

GIOM
Selected publications